Table of Contents
2048 Bit RSA and the Year 2030
In the course of some recent work I developed the impression that 2048 RSA was quite secure. Canada1) (my country of residence) and others 2) are currently strongly suggesting that 2048 bit RSA should be considered potentially insecure after the year 2030 and that the minimum length considered secure should be then be 3072 bits. That is only 7 years from now (2023).
Where did the 2030 cutoff come from?
I am reasonably certain that the ideas here came from an influential paper released in 2004 by Arjen K. Lenstra3) that showed this year in a table. Here is a simplified version of the table:
| Modulus Bit Length | Conservative Year | Optimistic Year |
|---|---|---|
| 1024 | 2006 | 2006 |
| 1280 | 2014 | 2017 |
| 1536 | 2020 | 2025 |
| 2048 | 2030 | 2040 |
| 3072 | 2046 | 2065 |
| 4096 | 2060 | 2085 |
| 8192 | 2100 | 2142 |
Common RSA modulus bit-length life spans. Table 4 from: Key Lengths
So we look at the 2048 bit row, decide we do not feel all that optimistic, and then choose 2030 as the cutoff date. Simple. Straightforward. Definite. Great for long term planning…
Lenstra's prediction was largely based on two observations:
- That the performance of computing technology was doubling every 18 months.
- That the increase of factoring efficiency due to software improvement was doubling every 18 months.
Combining the two observations means that as of 2004, the capability to attack RSA 2048 was doubling every 9 months. Then 2004 to 2030 is 26 years or 312 months or 35 doublings. That is a capability increase of 2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2×2 or 235 in exponential notation which works out to a predicted capability increase of 34,359,738,368 times as of 2030. So around 34 billion (34×109) times. This figure can be interpreted as how far 2048 bit RSA encryption was out of reach as of 2004. This is what that increase looks like on a plot:
Doubling every 9 months from 2004 to 2030
This sort of curve and this sort of increase is called “exponential” after exponential notation. It is well known that any physical quantity can not increase in this way past a certain point. There is a common and ancient story that illustrates this principle in a way quite appropriate to this discussion:
Someone is to be rewarded. As a reward, they ask that the following process be completed and that they should then be rewarded with the resultant number of wheat/rice grains.
Place a single grain on the first square of a chessboard. Place double that number of grains (2) on the next empty square. Then double that number of wheat grains (4) on the next empty square. If you fill all 64 squares of the chessboard, doubling each time, you end up with an amount of wheat some thousands of times more than the entire yearly production of wheat on the entire planet. Obviously this process can never be completed. The exponential nature of the increase precludes that4). An appropriate quote:
Exponentials can't go on forever, because they will gobble up everything.
Carl Sagan, Billions and Billions: Thoughts On Life And Death At the Brink Of The Millennium
Having seen that we have a predicted exponential increase of RSA factoring5) capability here, an important task will be to determine if a limit has yet occurred that would prevent that predicted increase.
How did things actually go?
The best we can do here is to look at the length of the numbers, of the sort relevant to RSA, that have been actually factored. So far, the largest number is 829 bits long6) which was factored in 2020. Late in 2003, a 576 bit number was factored. Here is a plot of those factoring achievements, including the ones between them:
I ignored the impression that the increase in factoring capability seems to have levelled off after 2009 and added a linear extrapolation based on the record factorizations over the entire predicted interval. The result (1024 bits by 2030) was still quite underwhelming. One would expect a more definite trend if the capability was increasing exponentially. The increasing trend is not enough to make us think that 2048 bit RSA would be under threat by 2030.
If the actual factoring demonstrations had shown a more definite upward trend then we could assume that the researchers were simply funded at a lower level than, say, some over funded state run signals intelligence agency and that there was the possibility of a genuine threat. But as it is, this is just inconclusive for our purposes. There are any number of reasons that less time and fewer resources might be allocated to these factoring demonstrations. We have to find another way to approach this question.
How are the basic assumptions holding up so far?
Let's consider the two basic assumptions that the prediction was based on:
Factoring Algorithm Performance
The assumption is that the increase of factoring efficiency due to software improvement will double every 18 months.
It isn't normally possible to predict the rate of software efficiency increase. It is safe to assume that there will be some increase of performance possible for a particular software system, but not how much or when. Software performance improvement, very generally, seems to have three phases:
| Phase | Performance Increase | Relative Complexity |
|---|---|---|
| Low hanging fruit | Large | Low |
| High hanging fruit | Low | High |
| New algorithm | Small to very large | — |
So improvement is first easy in the “low hanging fruit” phase and progressively harder in the “high hanging fruit” phase. The cost of this improvement is increased complexity. At some point someone might invent a new algorithm and the cycle can continue. The improvement that comes with a new algorithm can be very large; perhaps even enough to count as exponential if it happens more than once.
That is exactly what happened in the case of factoring algorithms in the '80s and '90s7). The continued fraction factoring algorithm was followed by the quadratic sieve factoring algorithm which was in turn followed by the number field sieve (NFS) algorithm. At the time of Lenstra's paper it seemed that his elliptic curve method might exceed the capability of the NFS algorithm.
For the 19 years from 2004 and 2023 and an assumption of 18 month doubling we end up with a predicted increase of algorithm performance of 6,502 times. It is hard to find definite figures on actual algorithm performance increase in this interval as it is mixed in with hardware performance. The CADO-NFS8) system claims a performance increase of 3.2 from version 1.1 to version 2.3.0 at the 512 bit (RSA-155) level. The researchers responsible for the most recent factoring record9) (829 bits) claimed a performance increase of 3-4 times. Even combining these improvements (I am not sure that is appropriate) we end up with a performance increase of 12 times which is well short of the predicted 6,502 times.
The elliptic curve method never ended up exceeding the NFS algorithm for factoring at the scale of RSA 2048. The NFS algorithm was never exceeded by any other invented algorithm. As a result the NFS algorithm is still the best available 27 years after its invention. That seems to be the reason for the severe slowdown in algorithm performance increase.
The history of computing shows that there is normally a quick burst of progress related to algorithmic performance when some particular task becomes feasible followed by a long period of very gradual improvement. The popular example of sorting is a good example. The mergesort, quicksort and heapsort algorithms were invented in 1945, 1959 and 1964 respectively. They are still in routine use today for sorting large lists of values. In retrospect it very much seems that the same sort of thing happened with respect to factoring algorithms. The complexity here seems to be high (CADO-NFS has hundreds of thousands of lines of code) so we are probably in the “high hanging fruit” phase. At this point there seems to be no reason to expect the predicted exponential increase in factoring algorithm performance (165,140 times) required to threaten 2048 bit RSA by the year 2030.
Computing Performance
The prediction is based in the assumption that the available computing performance will double every 18 months.
This assumption is popularly known as “Moore's Law”10). It has become fashionable to speculate that Moore's law is now dead. That is both true and false.
It turns out that there are two versions of Moore's law. The 18 month doubling refers to the increase in available computing performance and is appropriate to our discussion here. The original Moore's law refers to the number of transistors available on a substrate of a particular size and is now generally accepted to mean a doubling every 24 months. The 24 month law related to the number of transistors is still alive (but the rate of examples is decreasing rapidly). The 18 month performance law is the one that is dead. That's the one that the 2030 prediction is based on…
If you double the number of transistors on a substrate of a particular size then if the power consumption of those new transistors is half the power consumption of the old transistors then the result will be a substrate that produces the same amount of heat. Dennard scaling explains why this used to be the case. Otherwise, each doubling of transistors would produce more heat in the same area. That heat would quickly become unmanageable. The 18 month performance version of Moore's law depends on Dennard scaling to be practical. But Dennard scaling no longer works and as a result Moore's law 18 is dead.
This graph shows an example based on Intel processors:
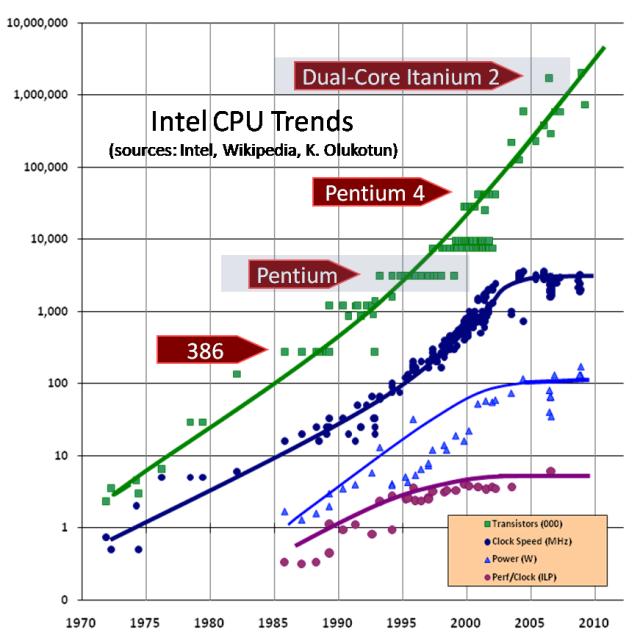
From: The death of CPU scaling: From one core to many -- and why we're still stuck
… which was from: The Free Lunch Is Over - A Fundamental Turn Toward Concurrency in Software
Note the logarithmic scale. The rising, roughly straight line for the number of transistors indicates that some sort of exponential increase is occurring. The qualities we are interested in, clock speed and performance per clock, have levelled off. The power consumption has levelled off because of physical limitations associated with removing heat from a substrate. Because of the end of Dennard scaling, performance is limited by the power efficiency of the transistors and the amount of heat that can be removed from the substrate. We can't make the transistors smaller in a way that would make them faster because making transistors smaller greatly decreases their power efficiency. That is mostly because of quantum tunnelling which turned out to be a fundamental physical limit on the performance of the highest performance computing technology we have.
There it is. A physical limit that prevents an exponential increase. In retrospect, it can be seen that this limit was already preventing an exponential increase in 2004 when the prediction was made. Unfortunate timing for the one making the prediction but it makes our task here easier. There was no exponential growth of computing performance from 2004 to 2023. It is very unlikely that such growth will reappear in the 7 years before 2030.
Where Are We Now?
How do things look for breaking 2048 bit RSA right now in 2023?
The best available algorithm known, usable with the most powerful computers we know how to build, is NFS. So we would use the NFS algorithm.
How much computing power could be brought to bear? As a exorbitant example we could use the Bitcoin mining network. The Bitcoin mining network is a distributed network devoted to breaking a cryptographic function with a brute force search. So it would seem to be a fairly good example to use with respect to breaking RSA which is the same sort of thing.
Bitcoin mining is a process that makes money for the entity running the mining system. This financial incentive has created a situation where the mining network has expanded to what might seem a ridiculous extent. The incentive is very sensitive to the cost of electricity. As a result the mining systems are designed to be as power efficient as humanly possible. The end of Dennard scaling is very relevant here. The troublesome heat starts as expensive electricity. Even with this desperate quest for energy efficiency, it is estimated that the Bitcoin mining network consumed 1/200th (0.5%) of all the electricity generated on the entire planet11)in 2021. This makes the network a good upper limit on what might be done in secret. If some over funded national signals intelligence agency built that much processing power we would be able to tell just by checking their power bill. Electricity consumption at the level of an entire country would be impossible to hide.
Let's imagine that we could magically repurpose the processing power of the entire Bitcoin mining network for breaking a single 2048 bit RSA key. This will require us to relate what the network is currently doing to the NFS algorithm. I will use the “apples to apples” relation developed in RFC376612). It's based on the situation in 2004 but there does not seem to be a better one available. The operations that the Bitcoin network performs would seem to take roughly the same amount of processing as the operations used as a reference in RFC376613). By RFC3766, breaking 2048 bit RSA would require 9.01×1030 cryptographic operations. The Bitcoin mining network recently achieved a rate of 1.24×1028 operations/year14).
So using the power of the largest amount of computing ever dedicated to breaking cryptographic operations in history, it would take 9.01×1030/1.24×1028 years to break one RSA key. That works out to 727 years. If we could magically create enough physical hardware to break a RSA key in a year then we would need to come up with 727/200 or 3.6 times the amount of electricity currently generated on the planet to run that hardware.
This only compares the amount of computing power required to break 2048 bit RSA vs the amount of computing power embodied by the Bitcoin mining network. The operations that the Bitcoin network do require very little memory/RAM. The NFS algorithm on the other hand requires a tremendous amount of memory. In 2004, R. D. Silverman pushed back against the idea that 1024 bit RSA was at imminent risk of compromise. As part of that argument he pointed out that the NFS algorithm has a phase (matrix reduction) that requires a large amount of computing power tightly coupled to a large amount of memory. On the basis of that observation he predicted that 1024 bit RSA would not be publicly broken before the 2030s. So far that prediction seems on track. In passing he mentioned that 2048 bit RSA would require 1018 bytes of memory for the irreducible matrix reduction step15). That's a million terabytes, an unimaginable amount of memory to be found in one place, much less tightly coupled to enough processing power to provide any practical benefit. Speaking of memory, the speed of DRAM has lagged to be something like a hundred times slower than processing and sieving is likely very cache unfriendly. So the idea that the processing power of the Bitcoin network could break a single 2048 bit RSA key in a mere 727 years is hopelessly optimistic.
It is clear that 2048 bit RSA is vastly out of the scope of current computing technology running the best available algorithm (NFS)…
The future
It appears that a fundamental algorithmic breakthrough would be a prerequisite to threaten the security of RSA 2048. How likely is such a breakthrough?
Factoring, prime numbers and the relationship between the two subjects have fascinated humanity for a very long time. The fundamental idea of sieving as a fast method of finding a lot of primes has been around for thousands of years16) (Number Field Sieve, Quadratic Sieve).
When creating advanced factoring algorithms there is a vast amount of historical knowledge available. This is very well trodden ground. I think this reduces the chances of surprising insights and reduces the advantage to those working in secret.
Quantum computing
Quantum computing of the sort intended to break RSA involves a breakthrough in both computing and algorithms. Normally some sort of new computing technology is invented and then algorithms are designed to enable that technology to do something useful. The quantum computing threat to RSA is different. We now have the algorithm (Shor's) but the computer to run it on only exists in our imagination.
If someone were to invent such a computer then RSA 2048 would be immediately and trivially breakable. RSA 3072 would also be trivially breakable. The same applies to RSA 4096 and 8192. The threat here is admittedly hypothetical, but this still serves as an example of a situation where routine key length extension is of no real value. By repeatedly increasing the size of keys we are betting that a breakthrough will be exactly strong enough to break the superseded key length and not break the current key length. That seems unlikely.
New threats tend to take a different form than old threats…
Conclusion
The assumptions that the 2030 date for increasing RSA key length were based on turned out to be invalid. A check of current capability confirms this. There seems to be no rational reason to increase RSA key sizes past 2048 starting in the year 2030. We don't have any reason to increase RSA key sizes at any time based on our current understanding.
Although this type of estimates is the best that can be done at this point, it should be understood that actual factoring capabilities may follow an entirely different pattern. Any prediction more than a few decades away about security levels is wishful thinking. The figures in the tables should be properly interpreted, namely as today’s best estimates that may have to be revised tomorrow. Anyone using factoring based asymmetric cryptosystems should constantly monitor and stay ahead of the developments in the research community.
The proceeding quoted text is found with the previously shown “Common RSA modulus bit-length life spans” table in the original paper. If you don't believe me you should still believe Dr. A. K. Lenstra, the one that came up with the double exponential prediction in the first place. We should enact a continuous process of watchful waiting. Any policy changes should be done as a response to changes in the algorithmic and computing performance landscape.
This is important because an aspect like a key length is often deeply embedded in the systems protected by the associated cryptography. Rooting out and changing such aspects is normally very expensive in the sorts of systems where cryptographic protection is provided. Where this is not possible at the software level then wholesale equipment replacement is required. The time and resources expended on pointless key length increases can be more profitably used elsewhere. Longer RSA keys require more processing power to process so that pointless keylength increases waste computing resources and power as well.
Other systems
Up to this point this article was made exclusively about RSA to improve readability. Let's use the ideas developed here to briefly examine some other popular cryptographic systems. I will use the NIST recommendations as the practical example17)18). The period for all of these NIST recommendations is from 2019 to 2030 (11 years). The current keysize recommendation became effective as of 2019 and the next one becomes effective as of 2030.
Discrete logarithm
Current group size: 2048 bits. Next group size: 3072 bits.
This is most often seen as the basis of the Diffie–Hellman key exchange system.
The best known algorithm to attack discrete logarithm systems is also a version of NFS. The difficulty vs RSA is slightly harder where the RSA key size is the same as the discrete logarithm group size. So the proceeding discussion about the pointlessness of increasing RSA key sizes directly applies to discrete logarithm systems.
Elliptic curve based
Current key size: 224 bits. Next key size: 256 bits.
The rule of thumb for elliptic curves is that 2 extra key bits doubles the difficulty. That's (256-224)/2=16 difficulty doublings over the 11 year period. So an implicit assumption that the capability available for breaking elliptic curves will double every 11*12/16=8.25 months. That's a bit faster than the 9 month double exponential assumption that in turn comes from the assumption that available processing power and algorithmic capability are each doubling every 18 months. We know that that is not true for processing power. I have not been able to find any indication of a current or upcoming breakthrough in software methods for breaking elliptic curves, but I am not really qualified to judge that. So I will have to leave this here. In the absence of any evidence of a algorithmic breakthrough then the increase from 224 bits to 256 bits would be unnecessary.
Elliptic curve based systems can use much shorter key lengths than other systems. Pointlessly increasing elliptic curve key length would be tragic. If the current assumptions are maintained that would mean we would see a recommendation for more than 256 bit elliptic curve keys for the 2040 decade.
Symmetric encryption
Current key size: 112 bits. Next key size: 128 bits.
Some examples of symmetric encryption schemes are: AES, ChaCha20 and Camellia.
One extra key bit doubles the difficulty here. That's 128-112=16 difficulty doublings over the 11 year period. So an implicit assumption that the capability available for breaking symmetric encryption will double every 11*12/16=8.25 months. That's a bit faster than the 9 month double exponential assumption that in turn comes from the assumption that available processing power and algorithmic capability are each doubling every 18 months. We know that that is not true for processing power.
The idea that the algorithmic capability against symmetric encryption might be doubling every 18 months is fairly surprising. A regular increase here is not something that is normally assumed. Perhaps there was some sort of “debt” with respect to key length that we are making up for in this time period. It might be good to apply the Bitcoin thought experiment as previously seen in this article as a sort of sanity check.
The number of cryptographic operations required to use brute force to break a 112 bit key in a symmetric system is 2112=5.19×1033 operations. We will make the reasonable assumption that one Bitcoin operation would take roughly the same time as one symmetric encryption operation. Then it would take 5.19×1033/1.24×1028=418,548 years. Reducing this to a year would require 418,548/200=2092 times the current total planetary electricity production19).
It does not seem reasonable to increase minimum symmetric encryption key size past 112 bits after 2030.
